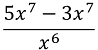Derivative
The basic concept of Derivatives
A derivative is a branch of calculus. It explains the rate
of change in dependent variables due to changes in independent variables. The
slope of variables can be derived from derivatives.
Let y = f(x) such that a very small change in independent variables x by del x leads to a change in independent variables y by del y. In this case, limit del x tends to zero and is called derivatives of y concerning x. For convenience, dy/dx can be used to perform a derivative. Economic decision-making has become more and more mathematically oriented due to numerous variables. The derivative is how the function changes when its input changes.
m = Change in y/Change in X
=dy/dx
Where dy = change in
y
dx = Change in x
In economics, x and
y are variables where one variable is the function of another variable. It
helps in finding the rate at which one quantity changes concerning another. It helps in finding maximum profit or minimum cost, etc.
Application of
Derivatives in Real Life
To calculate the
profit and loss in business using a graph.
To check the price,
demand, and loss in business using graphs.
To check the price,
demand, profit, etc.
To derive many
equations in economics.
In economics, we
strike with the word called marginal, which means change. Derivative takes the
responsibility of marginal as follows.
Marginal product =
dQ/ dL
Marginal cost = dC/
dQ
Marginal utility =
dU/dQ
Marginal revenue =
d(P.Q)/dQ
Where, Q = Quantity
of commodity
L = Labor
C = Cost function
U = Utility
R = P.Q = Revenue = Price x quantity
Similarly, Price elasticity Ep = dQ/dP x P/Q
Income elasticity Em = dQ/dM x M/Q
Cross elasticity Ec = dQm/dM x Py/Qx
Advertisement elasticity Ea = dQ/dA x A/Q
Where p = price, Q = output, M = consumer's money income, Py = Price of y, Qx = Quantity of x, and A = advertisement expenditure.
For handling
derivatives in economics, we must have some basic rules to follow.
Rules of calculation
of derivatives
The rules for
calculating derivative is known as the technique of differentiation.
Power rule:
Let y
= f(x) = xn
Differentiating
w.r.t x we get,
ⅆ𝑦/ⅆ𝑥 = nxn-1
For example, find
the derivative of x7.
Solution: Y = x7
Differentiating
w.r.t x we get,
ⅆ𝑦/ⅆ𝑥 = 7x7-1
= 7 x6.
Constant rule ( ⅆ𝑐/ⅆ𝑥=0)
Let Y = 5
Y = 5 x1
y = 5 x x0
Differentiating
concerning x, we get,
ⅆ𝑦/ⅆ𝑥=5 (ⅆx0)/ⅆ𝑥
=5. 0 x0-1
= 0
Find the derivative
of y = 6.
ⅆ𝑦/ⅆ𝑥=ⅆ𝟔/ⅆ𝑥=0
* Find the
derivative of y = x.
Differentiating
with respect to x, we get,
ⅆ𝑦/ⅆ𝑥=ⅆ𝑥/ⅆ𝑥
= (ⅆx1)/ⅆ𝑥
=1 x
1-1
=1⋅x0
=1.1
=1
Sum Difference rule:
If x has two functions, u and v
Let 𝒚=𝒖±𝒗
ⅆ𝒚/ⅆ𝒙=ⅆ(𝒖±𝒗)/ⅆ𝒙
ⅆ𝒚/ⅆ𝒙=ⅆ𝒖/ⅆ𝒙±ⅆ𝒗/ⅆ𝒙
*Find the derivative
of :𝑦=x3+4x2
ⅆ𝒚/ⅆ𝒙=ⅆ(x3±4x2 )/ⅆ𝒙
ⅆ𝒚/ⅆ𝒙=(ⅆx3)/ⅆ𝒙+(ⅆ4x2)/ⅆ𝒙
= 3x2+8𝑥
If y is a function of u and u is a function of x, then
Differentiating
Explicit and Implicit Functions
An explicit
function is given in terms of the independent variable.
Take the
following function:
y = x2
+ 3x - 8
y is the dependent variable and is given in terms of the independent variable x.
Implicit functions, on the other hand, are usually given in terms of both dependent and independent variables. eg:- y + x2 - 3x + 8 = 0 x+ y = xy
Demand
Function
The demand
function can be written in the form of an equation:
Qd = a — b.Px
where Qd is the quantity demanded
• a
is a constant – determined by non-price factors
• Px
is the price of the product x
Supply
Function
The supply
function can be written in the form of an equation
Qs = c +
d. Px
• Where
Qs is the quantity supplied
• c
= the level of supply independent of price
• Px
= the market price of the product x
d is the coefficient of price
Cost
Function
The cost
function is written as:
C(Q) = F +
V(Q)
C = Total
Expenses
Q = Number
of Units Produced
F = Fixed
Costs
V = Variable
Costs.
- fixed
costs remain unchanged despite the production level, including machinery costs, rent, or insurance payments.
- variable
costs, which include labor and materials, will change from time to time and
have a direct relationship to the level of production.
Average cost
(AC) =
C(Q)/Q
Where C(Q)
= total expenses
Q = Total quantity produced
Marginal
Cost
The
derivative of the cost function is called the marginal cost.
MC = dC/dQ
Revenue
Revenue is
the product of the price per unit times the number of units sold.
R = (P × Q)
Where P is the price per unit, R is the revenue and Q is the number of units sold.
Average
revenue
AR = R/Q =
PQ/Q =P
Marginal Revenue
The marginal revenue is the derivative of the revenue function.
MR = dR/dQ
Question: If
Rx = Q2 – 6Q +9 is the revenue function, find the demand and
marginal revenue of production level 9.
Solution: Given Rx = Q2 – 6Q +9
Differentiating
concerning Q, we get,
Marginal
revenue (MR) = d Rx/ dQ
= d (Q2 – 6Q +9)/dQ
= d Q2/dQ –
6 dQ/dQ +d9/dQ
= 2Q – 6
+0
= 2Q -6
=2x9 –
6
= 18 –
6
= 12
Now, PQ =R,
P = R/Q = Q2 – 6Q +9/Q
, P = Q – 6 +9/Q = 9 – 6 +9/9 = 4
Question: A
firm has a demand function P = 108 – 5Q and an average cost function (AC) =-12 +Q.
Find the marginal profit function and its value when Q= 8.
Solution:
P = 108 - 5Q
Revenue
(R) = P x Q
= (108 – 5Q) x Q
= 108Q – 5 Q2
Average cost
function (Ac) = Total expenses/ total quantity produced
-12 +Q =Total
expanses/Q
(-12+Q) Q = Total expenses
-12Q +Q2 = Total expenses
(Total cost)
Total Profit
= Total Revenue – Total Cost.
Profit π
= 108 Q–5Q2–(-12Q +Q2)
= 108Q – 5 Q2
+ 12Q –Q2
= 120Q – 6 Q2
Marginal
profit = dΠ/dQ
= d(120Q – 6Q2)/dQ
= 120 – 12Q
=120 – 12 x8
= 24
Marginal Propensity to consume (MPC) = dC/dY
The value of
MPC is always positive, but less than 1.
It decreases
as income increases.
MPC is
greater for the poor than that for the rich.
Demand is totally inelastic, which means it doesn't move at all when the price changes, according to the interpretation of E
E = 0. In these circumstances, the demand is inelastic because the percentage change in demand is less than the percentage change in price.
Demand is unit elastic if E = 1 (the percent change in demand is precisely the same as the percent change in price). For instance, a 10% price rise would result in a 10% drop in demand.
E > 1: The demand is elastic because it reacts to price increases more strongly than proportionately. Assume that a 15% rise in a product's price results in a 45% decrease in demand. E = 3 in this particular instance.
Degrees of Demand Cross elasticity Interpretation
Cross-elasticity of demand that is positive: (Exy>0) = substitute goods
Exy = 0 = Unrelated products for zero cross elasticity of demand.
Positive demand elasticity (Exy 0) = complementary goods